蒙特卡罗模拟用于在理论上不可能或不切实际地确定变量分布时估计变量的分布。它用于许多领域,包括工程、金融和 DFSS(六西格玛设计)。典型的蒙特卡罗模拟包括:(1)一个或多个输入变量X,其中一些通常遵循概率分布。(2) 一个或多个输出变量 Y,其分布是必需的。(3)耦合X和Y的数学模型。Statgraphics 还包括用于仿真模型的各种随机数生成器。
| 程序 | Statgraphics 百夫长 18/19 | Statgraphics Sigma express | Statgraphics stratus | Statgraphics Web 服务 | StatBeans |
|---|---|---|---|---|---|
| 通用仿真模型 |  |  | |||
| ARIMA 时间序列模型 |  | ||||
| 随机数生成 |  |  |  |  |  |
| 多元正态随机数 |  |
通用仿真模型
此过程用于查找由数学模型定义的一个或多个输出变量的分布,这些变量与多个输入变量之一耦合。可以指定每个输入变量的概率分布。主要输出包括输出变量的估计百分位数。
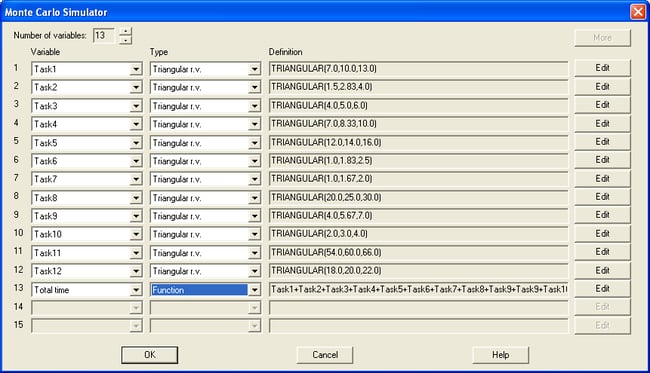
ARIMA 时间序列模型
此过程从 ARIMA 时间序列模型生成随机样本。
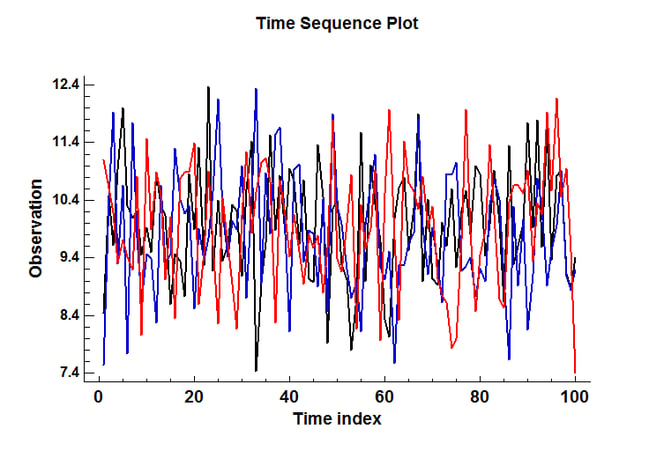
更多: Monte_Carlo_Simulation_ARIMA_Time_Series_Models.pdf
随机数生成
经常需要从不同的概率分布中生成随机数。此过程简化了创建多个随机数样本的过程。有 49 种概率分布可用。
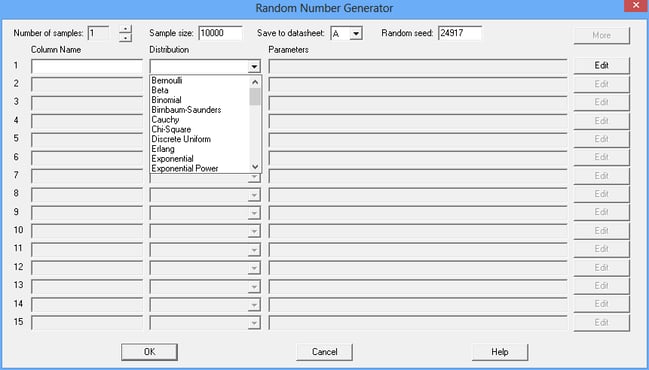
更多: Monte_Carlo_Simulation_Random_Number_Generation.pdf
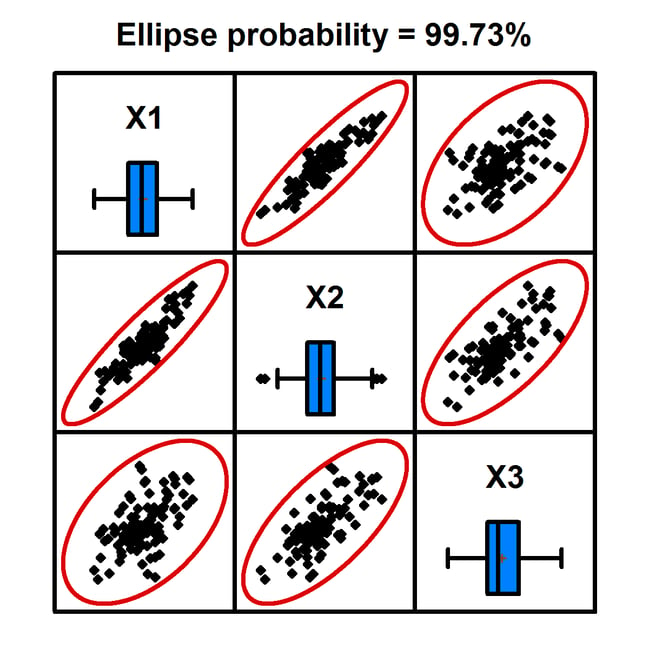
多元正态随机数
此过程从涉及最多 12 个变量的多元正态分布中生成随机数。用户输入变量均值、标准差和相关矩阵。生成随机样本,这些样本可以保存到 Statgraphics 数据手册中。