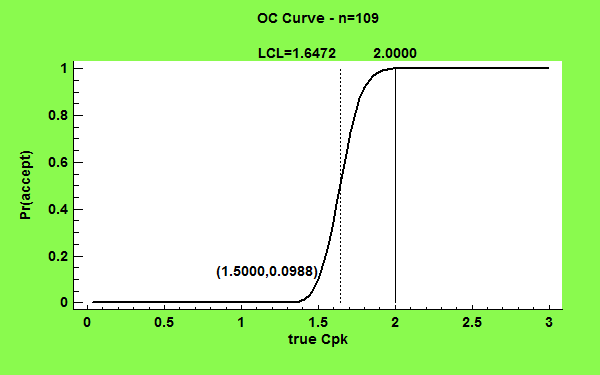
用于确定过程满足一组规范限制的程度的重要技术称为过程能力分析。能力分析基于从流程中获取的数据样本,通常产生:
1.DPMO(每百万个机会的缺陷数)的估计值。
2. 一个或多个能力指标。
3. 对流程运行的 Sigma 质量水平的估计。
STATGRAPHICS为以下情况提供能力分析:
| 程序 | Statgraphics Centurion 18/19 | Statgraphics Sigma Express | Statgraphics stratus | Statgraphics Web 服务 | StatBeans |
|---|---|---|---|---|---|
| 正态分布测量数据的能力分析 |  |  |  |  |  |
| 非正态分布测量数据的能力分析 |  |  |  |  |  |
| 相关测量的能力分析 |  | ||||
| 计数或比例的能力分析 |  | ||||
| 费率能力分析 |  | ||||
| 过程能力的贝叶斯估计 |  | ||||
| 能力指数的样本量确定 |  |
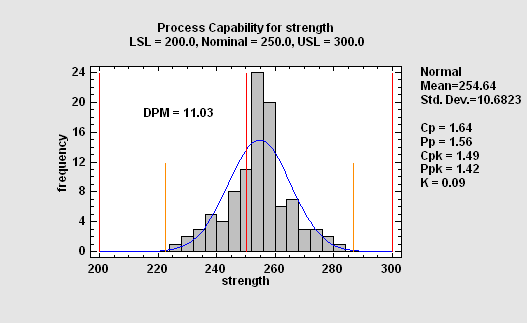
正态分布测量数据的能力分析
此过程对假定为正态分布中的随机样本的数据执行能力分析。它计算 Cpk 等功能指数,估计 DPM(每百万个缺陷数),并确定流程运行的 sigma 质量级别 (SQL)。它可以处理双侧对称规格限制、双侧非对称限制和单侧限制。还可以请求最常见能力指数的置信限。
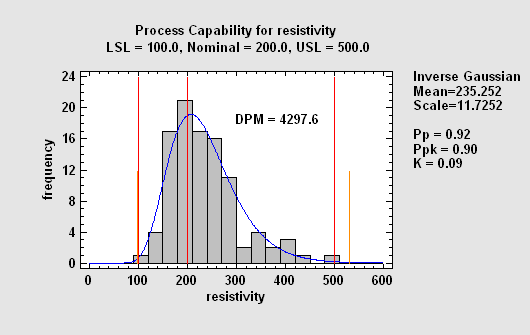
非正态分布测量数据的能力分析
此过程对未假定来自正态分布的数据执行能力分析。该程序将拟合多达 25 个备选分布,并根据它们的拟合优度列出它们。然后,对于选定的分布,它会计算等效的能力指数、DPM 和 SQL。
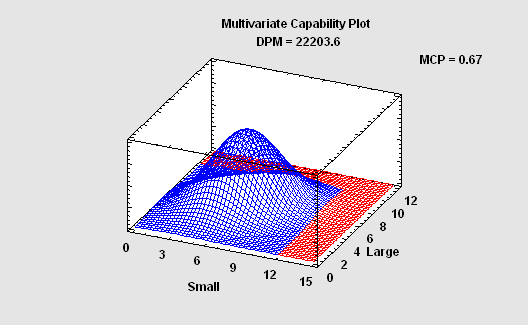
相关测量的能力分析
当表征过程的变量相互关联时,单独估计每个变量的能力可能会严重扭曲过程的执行情况。在这种情况下,有必要估计一个或多个变量超出规范的联合概率。这需要拟合多变量概率分布。此过程基于多元正态分布计算能力指数、DPM 和 SQL。
计数或比例的能力分析
当对项目或事件的检查导致通过或失败而不是测量时,过程能力分析必须基于离散分布。对于非常大的手数,相关分布是二项式。对于小批量或失败机会有限的情况,必须使用超几何分布:
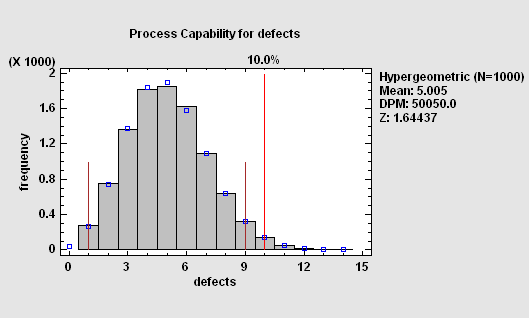
比率能力分析
当相关的性能度量是速率时,过程能力分析基于:如果故障随机发生,则为泊松分布;如果故障往往成团发生,则为负二项分布。
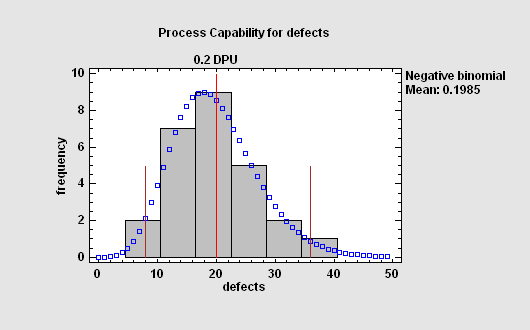
过程能力的贝叶斯估计
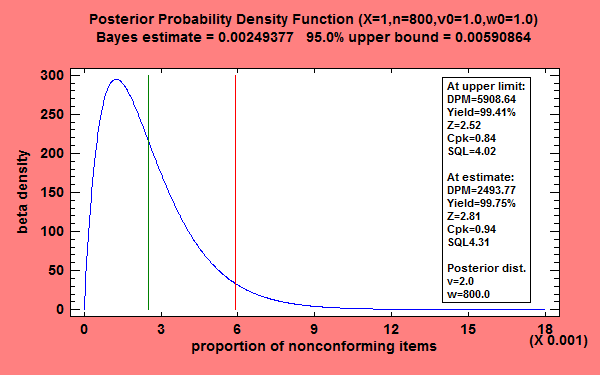
当存在关于过程生成的不合格项的可能比例的先验知识时,贝叶斯方法来估计过程能力可以提供比仅依赖新数据样本更精确的估计。将先验知识与当前数据相结合,可以创建后验分布,可用于创建过程能力的点和区间估计。
更多: Attribute Capability Analysis Statlet.pdf 或 Watch Video
能力指数的样本量确定
此过程确定用于估计三个能力指数(Cp、Cpk 和 Cpm)的合适样本量。该确定基于估计值的所需精度或假设检验的功效。