Statgraphics 中使用最频繁的部分之一是包含回归分析过程的部分。每个过程都旨在根据一个或多个因子的值预测因变量 Y 的值。根据 Y 中的数据类型,用户可以选择:
1. 对于连续 Y,一般线性模型、非线性回归、正交回归等过程。
2. 对于二元 Y 或比例,逻辑回归和概率分析等程序。
3. 对于计数数据,泊松回归、负二项式回归和零膨胀计数回归等过程。
4. 对于寿命数据或失效时间,采用考克斯比例风险或寿命数据回归等程序。
最新版本的 Statgraphics (V19.5) 包含 2 个新过程,用于在 Y 为分类时拟合回归模型:
5. 当 Y 由有序类别组成时的序数回归。
6. 当 Y 由无序类别组成或序数回归的比例赔率假设不成立时,多项式 Logistic 回归。
有序回归
例如,UCI机器学习存储库包含一个数据集,其中对2所西班牙大学的913名教职员工进行了调查,了解他们对维基百科有用性的看法。他们被问到一系列问题,他们使用以下李克特量表回答:
1 = 非常不同意
2 = 不同意
3 = 中性
4 = 同意
5 = 非常同意
在这种情况下,响应是有序的。每位教职员工还以多种方式进行分类:
年龄:数字
性别:男性或女性
领域:1 = 艺术与人文; 2=科学; 3=健康科学; 4=工程与建筑; 5=法律与政治
博士:0=否;1=是
YEARSEXP(大学教学经验年限):数字
大学:1=UOC; 2=UPF
这里的目标是根据这些因素为教职员工的反应开发一个预测模型。
在这篇博客中,我们将专注于对以下声明的回应,标记为 Qu1:“维基百科中的文章是可靠的。我们将从一个非常简单的模型开始,该模型仅涉及一个预测因素:AGE。让 Y 取 1 到 5 之间的 k 个值,我们将首先使用 logit 变换转换 Y ≤ j 的概率
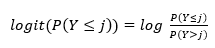
logit 变换是 Y 小于或等于 j 的几率的对数。在有序回归模型中,logit 变换与预测变量相关,根据
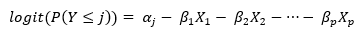
有一个单独的拦截αj对于 Y 的前 k-1 个唯一值和 X 的每个 p 值的公共参数。每个截距对应于序数变量 Y 的水平之间的断点,在本例中,在 s 之间,不一致与不同意之间,不同意与中立 之间,依此类推。每个定量预测变量都有一个 β 参数,具有 m 水平的分类因子有一个 (m-1 β) 个参数。请注意,每个β系数前面都有一个负号。这是有意为之的,因此当β为正时,增加 X 的值会导致 Y ≤ j 的几率降低,这对应于更有利的响应。
检查模型时,应该注意的是,预测变量的效应不依赖于 j。logit 曲线作为 X 的函数,只需在每个断点处向上移动。这称为比例赔率或平行回归假设。如果这个假设站不住脚,那么我们就需要做一个完全多项式拟合,它不依赖于序数数据的特殊结构。
为了在 Statgraphics 中分析这些数据,我们将从一个仅涉及 AGE 的模型开始。Statgraphics 调用 R 中的 POLR 函数来执行计算,这将返回下表:

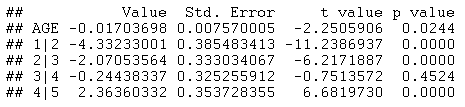
AGE 的小 P 值表明年龄对响应的影响在 5% 显著性水平上具有统计学意义。负系数表示 AGE 对小于或等于 j 的几率有正向影响(回想一下,模型在每个系数之前都包含负号)。这表明年长的教职员工对维基百科的可靠性持不太好的态度。
可以通过解码拟合模型并绘制 Y = j 的每个值的概率来检查拟合模型:
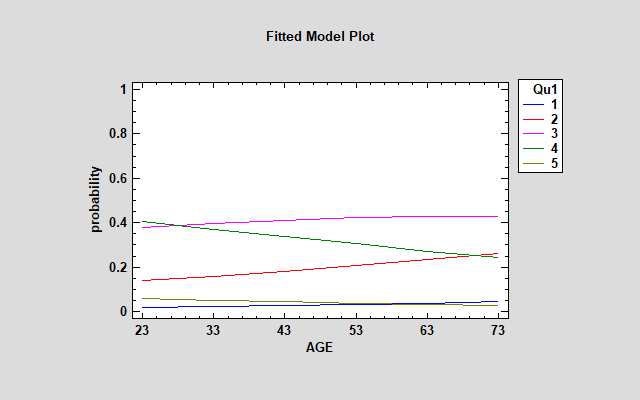
AGE 的影响在 j = 2 和 4 时尤为明显。年长的教职员工更有可能“不同意”,而年轻教职员工更有可能“同意”。
为了使模型更有趣,我们现在将引入性别作为分类因子。从以下输出中可以看出,GENDER 在 5% 的显著性水平上也具有统计学意义:

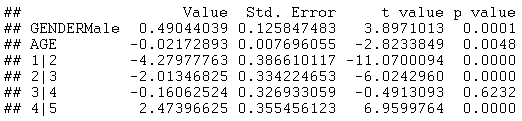
GENDERMale 上的正值表示当 GENDER = Male 时,logit 函数的值下降 0.49。这相当于更有利的回应。在格子图中绘制概率时,雄性和雌性之间的差异非常明显:
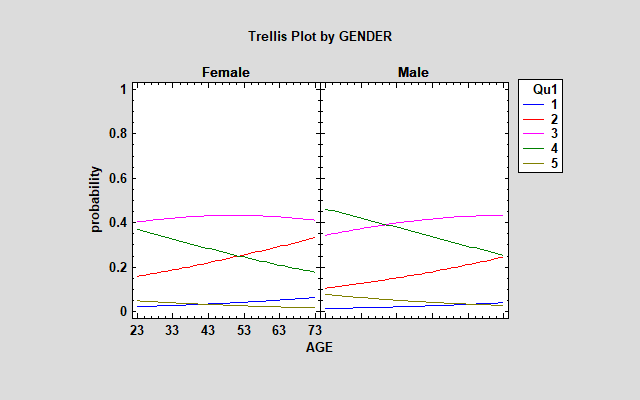
女性更有可能回答“不同意”或“非常不同意”,而男性则回答“同意”或“非常同意”。
可以通过查看 Akaike 信息准则 (AIC) 来比较不同的模型。AIC 是考虑估计参数数量的预测误差的估计值。由于第二个模型的 AIC 值较低,因此它比第一个模型更可取。
在拟合有序回归模型时,还可以设置各种选项,如“分析选项”对话框中所示:
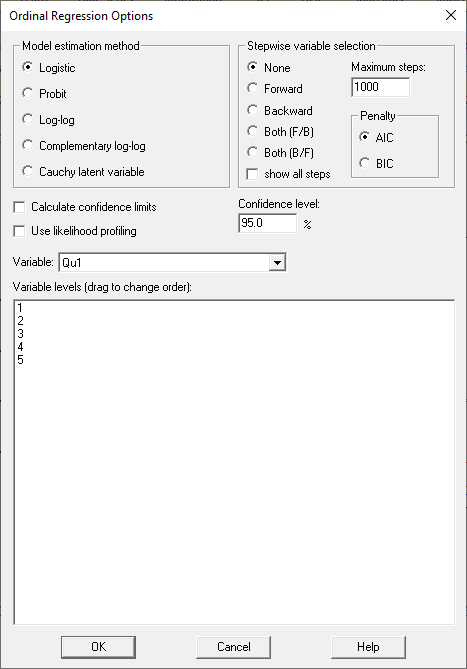
可以使用其他链接函数(如 Probit)来代替使用逻辑转换。有人建议:
1. 当所有类别具有相似的概率时,使用逻辑。
2. 当较低类别占主导地位时,使用 log-log 函数。
3. 当较高类别占主导地位时,使用互补的对数-对数函数。
4. 当存在极值时,使用柯西潜在变量变换。
此外,可以进行逐步变量选择以选择可能的预测变量的子集。将 DOMAIN、PhD、YEARSEXP 和 UNIVERSITY 添加到模型中,然后选择“前向逐步变量选择”将生成以下模型:
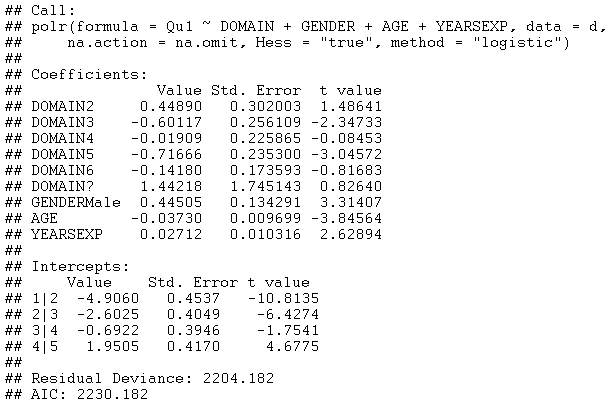
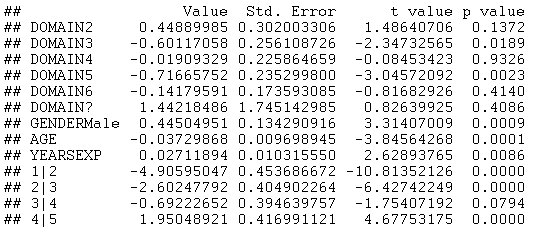
除PhD和UNIVERSITY外的所有变量均通过逐步变量选择程序进行选择。DOMAIN3和DOMAIN5上的大负系数特别有趣。它们意味着这些领域的教职员工比其他人更有可能对维基百科文章的可靠性持负面看法。
多项式回归
如果因变量 Y 的 k 个类别没有自然顺序,则必须进行多项式回归而不是有序回归。这涉及拟合表单的模型
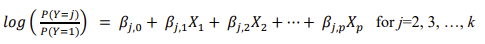
该模型描述了预测因子对类别 j 的概率与类别 1 的概率之比的影响。除类别 1 外,每个类别都有一整套β。请注意,这允许每个类别的因子效应不同。
Statgraphics 通过调用 R 中的 multinom 函数来拟合此类模型。对于涉及 AGE 和 GENDER 的模型,输出如下所示:
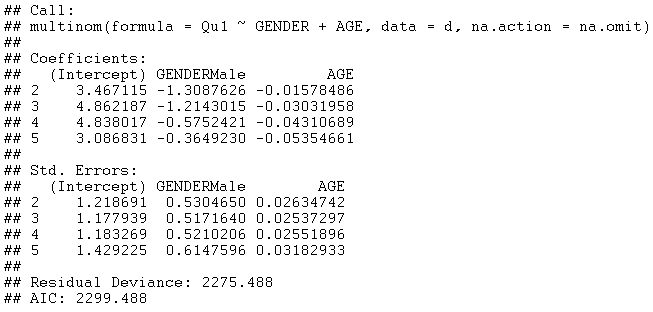
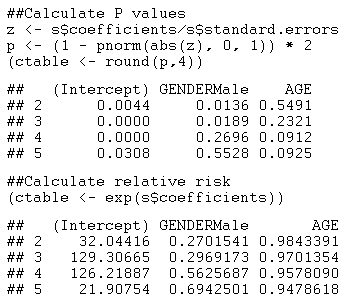
该模型的参数数量是序数回归模型的两倍(12 对 6)。AIC略小(2299.488对2301.827)。请注意,每个 GENDERMale 的估计系数在响应 2 到 5 之间差异很大。
检查此模型的格子图,您将注意到估计概率的基本模式与有序回归模型相同。
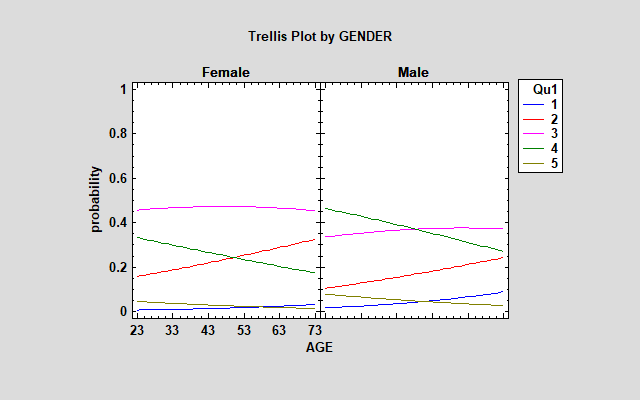
然而,老年男性的蓝线比序数模型高得多。比较有序回归和多项式回归结果的一种有趣方法是保存两个模型中每个教职员工的估计概率,并构建如下所示的图:
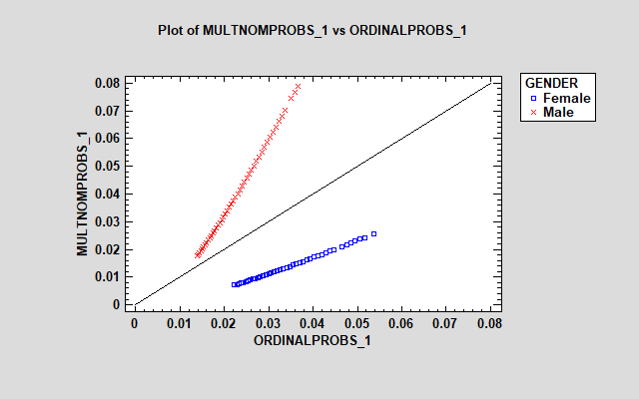
该图显示了每个人根据其年龄和性别做出“强烈不同意”的估计概率。多项式回归模型预测男性的概率要高得多,而序数模型预测女性的概率要高得多。在多项式模型中,年龄的影响(由点的范围显示)对于男性也更为明显。可以为每个其他响应生成类似的图。
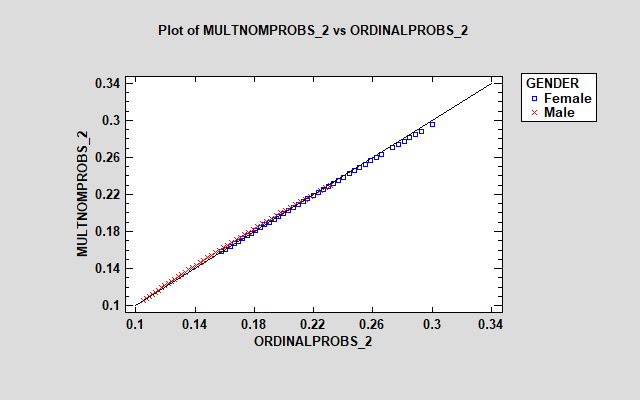
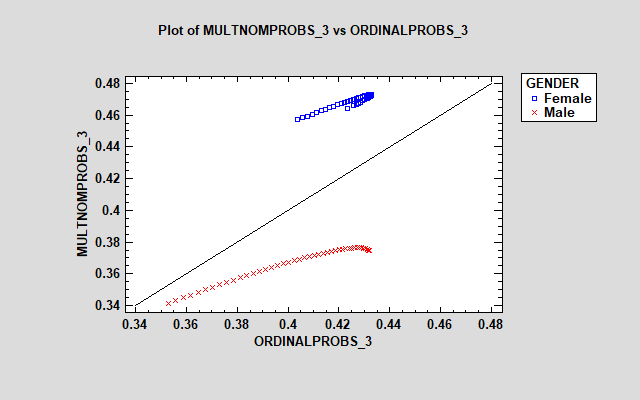
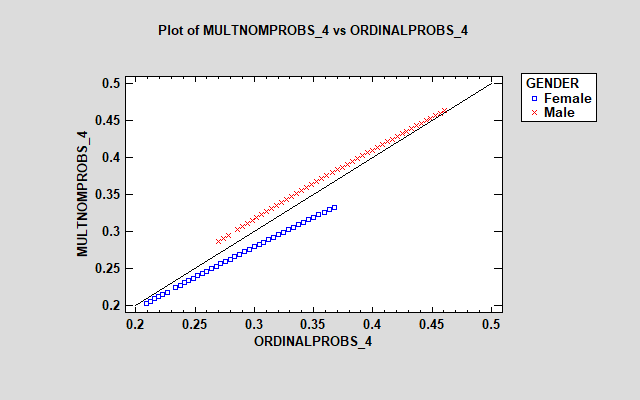
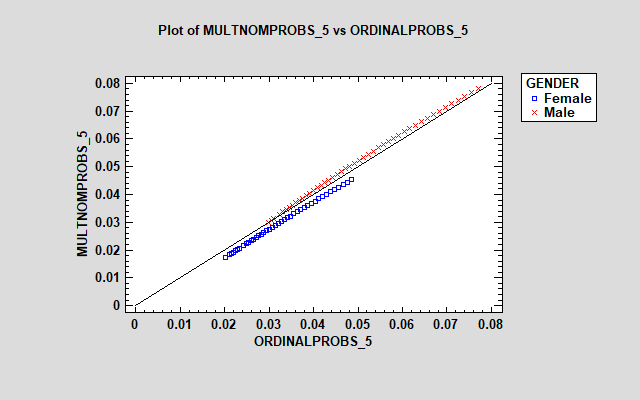
对于响应 2、4 和 5,这些模型相当相似。然而,“中性”响应的模型之间存在很大差异 (3),多项式模型显示女性的估计概率要大得多。多项式模型中的附加参数使其能够以不同的方式处理因子对每个响应的影响。
为了确定多项式模型的附加参数是否可以在统计上证明其合理性,可以从残差偏差中计算近似似然比检验:
G = 2289.827 – 2275.488 = 14.339
可以将其与具有 12-6 = 6 个自由度的卡方分布进行比较。该统计量的 P 值约为 0.026,因此得出的结论是,多项式模型在 5% 的显著性水平上更可取。
引用
数据来源:Dua, D. and Graff, C. (2019)。UCI 机器学习存储库 [http://archive.ics.uci.edu/ml]。加利福尼亚州尔湾:加州大学信息与计算机科学学院。https://archive.ics.uci.edu/ml/datasets/wiki4he
引自:Meseguer, A., Aibar, E., Lladós, J., Minguillón, J., Lerga, M. (2015).影响维基百科在高等教育中的教学使用的因素。JASIST,信息科学与技术协会杂志。国际标准刊号:2330-1635。doi: 10.1002/asi.23488.